9594. ABA
The string of
letters is given. How many times the subsequence “ABA” occurs in the given
string? The letters “ABA” may not be adjacent, but their order must be
preserved.
Input. One line containing only uppercase Latin
letters. The length of the string does not exceed 106.
Output. Print the number of occurrences of the subsequence
“ABA” in the string.
|
Sample
input 1 |
Sample
output 1 |
|
YARBRBAQ |
2 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
ABAYBATATBBAZA |
29 |
SOLUTION
combinatorics
Algorithm analysis
Let s0s1…sn-1 be the input string. Let l[i] contain the number of letters A in
positions from zero to the i-th
inclusive. Let cnt
be the number of the letters A in the word. Then to
the right of position i there are cnt – l[i] letters A.

If the letter B is in the i-th position, then to the left of it,
there are l[i] letters A, and to the
right, there are (cnt – l[i]) letters A. The number of
subsequences “ABA” in which the letter B is in the i-th position equals to l[i]
* (cnt – l[i]).
The remaining task is to sum up the values
of l[i] * (cnt – l[i]) for all positions i where the letter B is located.
Second solution. Iterate through the input string from left
to right and count the number of letters A in the variable a.
For each letter B in the string, there exist a words AB (there are exactly a letters
A preceding the current letter B). Count the number of encountered words AB in
the variable ab. Increment ab by a for each letter B.
For each current letter A, there exist ab
words AB preceding it. Count the number of encountered ABA words in the
variable aba. Increment aba by ab for each letter A.

Example
Consider the second test case.
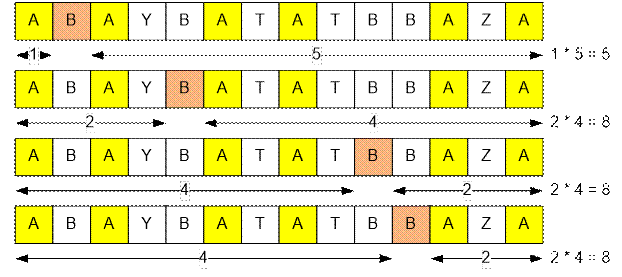
The number of
subsequences “ABA” is
1 * 5 + 2 * 4 + 2
* 4 + 2 * 4 = 5 + 8 + 8 + 8 = 29
Let’s examine the values of the variables
in the case of solving the problem using the second method.

Algorithm implementation
Read the
input string s.
cin >> s;
Initialize
the variables.
cnt = 0; len = s.size();
l.resize(len);
For each
position i, store in l[i] the number of letters A in positions
from zero to the i-th inclusive. At the end of the loop, cnt contains the number of A.
for (i = 0; i < len; i++)
{
if (s[i] == 'A')
cnt++;
l[i] =
cnt;
}
Compute the
answer in the variable res.
res = 0;
Count the
number of subsequences “ABA” for each position i that contains the letter B.
for (i = 0; i < len; i++)
if (s[i] == 'B') res
+= 1LL * l[i] * (cnt - l[i]);
Print the
answer.
cout << res;
Algorithm implementation – combinatorics
Read the
input string s.
cin >> s;
Initialize
the variables.
a = ab =
aba = 0;
Iterate
through the characters of a string and recalculate the variables a, ab
and aba.
for (i = 0; i < s.size(); i++)
if (s[i] == 'A')
{
a++;
aba += ab;
}
else
if (s[i] == 'B') ab += a;
Print the
answer.
cout << aba << endl;
Python implementation
Read the
input string s.
s = input()
Initialize
the variables.
cnt = 0
n = len(s)
l = [0] * n
For each
position i, store in l[i] the number of letters A in positions
from zero to the i-th inclusive. At the end of the loop, cnt contains the number of A.
for i in range(n):
if s[i] == 'A':
cnt += 1
l[i] = cnt
Compute the
answer in the variable res.
res = 0
For each
position i, that contains letter B,
count the number of subsequences “ABA”.
for i in range(n):
if s[i] == 'B':
res += l[i] * (cnt - l[i])
Print the
answer.
print(res)
Python implementation –
combinatorics
Read the
input string s.
s = input()
Initialize
the variables.
a = ab = aba = 0
Iterate
through the characters of a string and recalculate the variables a, ab
and aba.
for c in s:
if c == 'A':
a += 1
aba += ab
if c == 'B':
ab += a
Print the
answer.
print(aba)